Small Data
Welcome to another edition of “In the Minds of Our Analysts.”
At System2, we foster a culture of encouraging our team to express their thoughts, investigate, pen down, and share their perspectives on various topics. This series provides a space for our analysts to showcase their insights.
All opinions expressed by System2 employees and their guests are solely their own and do not reflect the opinions of System2. This post is for informational purposes only and should not be relied upon as a basis for investment decisions. Clients of System2 may maintain positions in the securities discussed in this post.
Today’s post was written by Seth Leonard.
Overview
One hears a lot about “Big Data.” Everyone seems to want to use it, in combination with AI, to print money and retire at 35. Big data is something System2 deals with every day. Definitions can be a little loose, but a useful criterion is simply more data than can be stored in memory: transaction data, location data, app, and web data. All of these can have billions of rows. That’s a lot to keep track of, and it requires careful thought to extract meaningful conclusions from all the noise. But what if someone asks you to come up with a forecast for direct-to-consumer revenue for Canada Goose? Or Allbirds? Historical revenue data can be pretty limited; typically, we’re dealing with 15 to 30 quarterly observations. How do we take big data and use it to forecast small data? This article highlights two issues that come up often when working with small quarterly frequency data: seasonal and persistent errors.
Big Data to Small Data
Because this piece is about small data, I’ll gloss over the details of how to get from big data to a few quarterly observations. In short, we need to tag data to ensure we’re getting the observations we want, panel it to make sure it’s representative of the wider population and comparable from one period to the next, and add it up to the frequency we want — quarterly in this case. That leaves us with one left-hand side (LHS) series we want to predict (revenue for example) and one right-hand side (RHS) series to use to build our forecast (aggregated transaction data for example). In practice, we’ll actually construct a number of forecasts and pool them as a means of reducing out-of-sample error. But instead of going through the whole process, I’ll highlight a few specific issues and describe how to deal with them.
Seasonal Errors
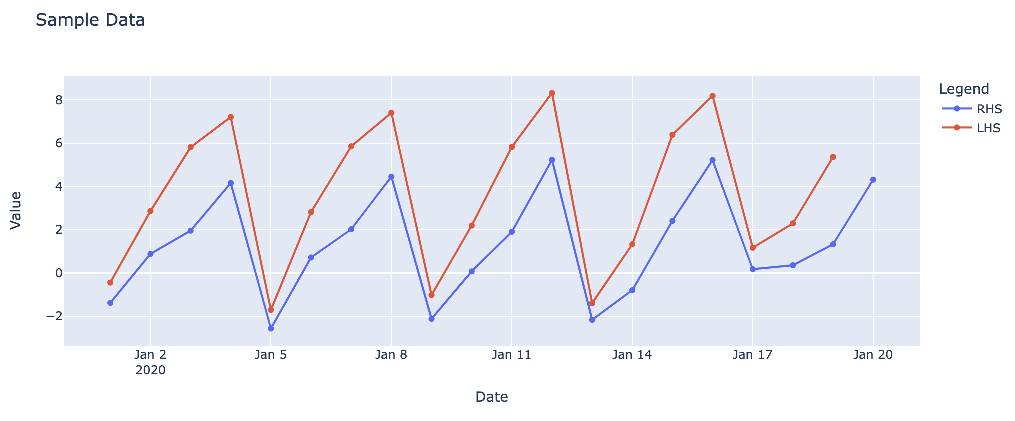
Here’s a simple example using simulated data of what quarterly revenue against one of our RHS series might look like.
Note the seasonality in the data. It’s common practice to transform numbers like this to year-on-year (YoY) percent change to remove these seasonal effects. It’s certainly worth looking at YoY forecasts (System2 does), but YoY data has some disadvantages. First, we’ll be losing four observations (which comes with quarterly data); when we only have 20 or so observations to begin with, that matters. And YoY data obviously depends a lot on what happened a year ago, which may not be the best indicator of what’s happening now. The impact of seasonality is more obvious if we fit our RHS data via OLS regression:
Clearly, errors follow a regular pattern. Sophisticated seasonal adjustments like X-13ARIMA SEATS are out as there are too few observations. Instead, we do the simple and obvious thing: calculate the average error for each quarter and add it back into our forecasts. By definition, this will improve things in sample, so it’s worth being cautious about error bounds and backtesting for at least a few periods.
This sounds a lot like adding quarter dummies (which is a good idea depending on the number of observations we have), but there’s a slight difference. This approach calculates seasonal errors after fitting; adding quarter dummies in the OLS regression is more prone to overfitting as you’re adding right-hand side variables (i.e., reducing degrees of freedom in frequentest terms). Alternatively, a seasonal ARIMA model might be a good choice (more on ARIMA below). Again, the limiting factor here is the number of historical observations. Numerically maximizing an ARIMA likelihood function will certainly lead to a good in-sample fit, but with few observations out-of-sample estimates may be poor. Sometimes, simple really is better.
Persistent Errors
Another potential problem that comes up with trying to match alternative data to reported numbers is persistent errors. This can happen a number of ways, but the most obvious issue is that the panel doesn’t line up exactly with the shopping public. For example, suppose we only observe credit card spend, and that consumers are tending more towards using credit cards and less towards using cash or debit cards. Over time, our panel would make it look like spend is growing more than it is. Or, going the other way, consumers might be moving more towards using buy now pay later services, in which case our observed spend could be decreasing. We address these issues on a case by case basis, but if the change in behavior has been persistent over time then including autoregressive errors in our model can help improve forecasts. As a simple example, here’s what that might look like:
Note that errors (in light blue) start off negative but become positive. As before, our concern is overfitting in sample, so we’ll try as much as possible to keep the model simple. In this case, we have two equations:
We could, of course, use more lags of errors, but because we’re dealing with so few observations this again increases the risk of overfitting in sample.
The simplest (programmatically at least) way to deal with this model is to cast it as an ARIMAX model using pre-built code. However, doing so ignores a restriction we can impose on the model. Doing a wee bit of algebra we have:
Where γ = α + a - bα is just a constant term. Thus, we only need to estimate three parameters (plus a variance term); since we’re concerned with having few observations, that extra restriction counts for a lot. Finding the maximum likelihood (remember when that’s what ML used to mean!?) is a simple numerical optimization problem (and ARIMA models numerically optimize the model — typically in state space form — anyhow). The result is a much better fit, with a mean squared error of 0.48 versus 1.68:
Our model doesn’t get worse at the end of the sample, an important consideration when we’re trying to forecast the next period! Again, we’ve added an extra parameter (but only one!), so be cautious of overfitting in sample.